| |
| ||
       |
 |
 |
|
|
 |
 |
 |
|
 | |||
| |||||
|
|
This Document | | ||
|
|
| |||
| |||||
|
|
 |
SummaryPlus | |
|
|
|
 |
Full Text + Links | |
|
|
|
·Full Size Images | |
| |
|
|
|
PDF (640 K) | |
|
|
|
| |||
| |||||
|
|
| |||
|
|
Actions | | ||
|
|
| |||
| |||||
|
|
|
Cited By | | |
|
|
|
Save as Citation Alert | | |
|
|
|
E-mail Article | | |
|
|
|
Export Citation | | |
 |
|
 | |||
| |||||
An analytic modelling approach for network routing algorithms that use
“ant-like” mobile agents
Nigel Beana
and Andre Costaa,
b,
, 
aApplied
Mathematics, University of Adelaide, Adelaide 5005, Australia
bCentre of Excellence for Mathematics and Statistics of
Complex Systems, University of Melbourne, Melbourne 3010, Australia
Received 23 May 2004; revised 20 October 2004; accepted 10
January 2005. Responsible Editor: F. Cuomo. Available online 22
February 2005.
In this paper, we introduce an analytic modelling approach to the study of a novel class of adaptive network routing algorithm, which is inspired by the emergent problem-solving behaviours observed in biological ant colonies. This class of algorithm utilizes “ant-like” agents which traverse the network and collectively construct routing policies. Previous studies have focused exclusively on simulation experiments, which indicate that such algorithms perform well in response to real-time changes in traffic demands and network conditions. The analytic model presented in this paper permits useful insights into certain fundamental aspects of ant-based algorithms, which have not been discussed in previous ant-based routing literature. In particular, the work presented in this paper motivates our proposal of a number of modifications to the basic design of ant-based routing algorithms, which result in improved performance with respect to equilibrium performance measures.
Keywords: Adaptive routing; Ant-based routing; Reinforcement
learning; Wardrop equilibria
From the days of the earliest distributed computer networks, through to the present-day Internet, interest in adaptive and decentralized systems for routing control in networks has driven the development of algorithms which aim to dynamically reconfigure a traffic routing policy, in response to real-time changes in traffic demands and network conditions. Examples range from the Distributed Bellman–Ford Algorithm [1], to more recent routing schemes based on reinforcement learning and stochastic optimization [2], [3], [4] and [5].
Within this context, an interesting and novel contribution has stemmed from a recently-developed and well-established stochastic optimization meta-heuristic known as Ant Colony Optimisation [6] and [7], which takes its inspiration from the collective problem-solving behaviours observed in biological ant colonies. The application of this meta-heuristic to the problem of adaptive routing and load-balancing in communications networks has led to the development of a number of dynamic routing algorithms which employ “ant-like” mobile agents [8], [9], [10], [11] and [12]. These algorithms, known as ant-based routing algorithms, attempt to reproduce in the artificial system some of the collective problem solving abilities that have been extensively observed and documented in the biological counterpart (see [6] for examples and references).
As noted in the recent survey paper [13], research carried out in the area of ant-based routing algorithms has so far been restricted to simulation-based modelling and analysis. Most notably, the simulation studies presented in [9] indicate that ant-based routing algorithms perform well when compared against standard routing algorithms currently employed in the Internet, such as Distributed Bellman–Ford [1] and OSPF [14], which are typically used in conjunction with shortest path routing [1]. The focus of such simulation studies has been on transient measures of performance in response to sudden changes in traffic demands and network conditions [9]. While such considerations are very important for the study of any adaptive routing algorithm, we show in this paper that a great deal of useful information and insight can be gained from the study of equilibrium (steady-state) properties of ant-based routing algorithms. In particular, we present an analytic modelling approach for the study of ant-based routing algorithms, which serves to draw attention to a number of theoretical aspects that have not been made readily apparent through the simulation-based research carried out to date.
By drawing on aspects of reinforcement learning [2], game theory [15] and non-linear optimisation [16], we identify a number of inefficiencies that are inherent in the current design of ant-based routing algorithms. Specifically, we highlight the fact that ant-based routing algorithms are on-policy learning algorithms [2], in the sense that the mechanism for performing exploration of alternative routing decisions is not entirely separate from the mechanism used to make routing decisions. We argue that this is an undesirable aspect of ant-based routing algorithms, and we propose simple modifications which render the ant-based approach off-policy [2], in the sense that the mechanisms for exploration and decision-making are completely de-coupled without compromising either of these tasks.
Furthermore, we compare the routing policies generated by ant-based routing algorithms with user and system-optimal routing concepts. The insight gained through this analysis leads us to propose changes to the design of ant-based routing algorithms which improve their performance with respect to equilibrium measures of network delay. In particular, we show that subject to certain modifications, ant-based routing algorithms are able to achieve a type of user-optimised routing known as the Wardrop equilibrium [17].
Importantly, we note that the modifications that we propose in this paper complement, but do not compromise, the desirable features of ant-based routing algorithms which have made them appealing to researchers in the field of communications networks (and indeed the wider scientific community [18]), these being their transient adaptive properties, robustness, and decentralized structure.
This paper is organized as follows. Section 2 provides a brief introduction to the collective shortest-path finding behaviours observed in biological ant colonies, that have inspired the development of ant-based routing algorithms for communications networks. Section 3 provides an overview of the major ant-based routing algorithms that have been proposed in the literature, and in Section 4, we describe an ant-based algorithm for routing in connectionless packet switching networks [1] which forms the basis for the analysis presented in this paper.
In Section 5, we present an analytic model which captures the equilibrium behaviour and certain transient properties of the algorithm described in Section 4. Our analysis of ant-based routing algorithms via an analytic model is presented in two parts.
For the first part, in Section 6, we consider the special case where there are no data traffic demands placed on the network. This context provides a simple vehicle for investigating the effect that the on-policy property has on the ability of ants to accurately learn about network delays. The second part of our analysis is presented in Section 7, where we consider the usual case where data traffic demands are placed on the network. In this context, we are able to investigate the ability of ant-based algorithms to perform load-balancing of traffic over multiple routes.
We propose and analyse an improved off-policy version of the ant-based routing algorithm in Section 8. Conclusions and discussion follow in Section 9.
Biological ants possess many qualities which are desirable in artificial systems, from an engineering point of view [6]. Individually they operate using simple rules, while collectively they are able to form complex patterns as “solutions” to the problem of finding food sources. Furthermore, ants function much of the time without centralized control, which means that an ant colony is in many ways a distributed system carrying out decentralized computation.
An interesting experiment carried out in the laboratory, is known as the double-bridge experiment [19]. It serves to highlight how the simple rules followed by individual ants are able to give rise to a collective “decision-making” process. In relation to this particular experiment, ants have been observed to follow rules, which can be summarized as:
• ants deposit (chemical) pheromone at an approximately constant rate as they travel,1 and
• ants are able to detect differences in pheromone concentration in their surroundings, and will tend to move in the direction where the concentration is highest.
In addition, as in many natural systems, there exists some degree of random fluctuation. This may cause individual ants to follow a path with a lower or even zero pheromone concentration level. This type of behaviour is referred to as exploration. Furthermore, pheromone evaporates or decays at an approximately constant rate, which means that trails must receive continual reinforcement in order to remain in existence.
In the double bridge experiment, ants are allowed to establish a pheromone trail between their nest and a food source. An obstacle is then placed in the path of the ants, in such a way that the ants have a choice of two paths around the obstruction, one of which is twice as long as the other. Initially, there is no pheromone on either the long or short path, and therefore ants have equal probabilities of choosing either path. This results in approximately half of the ants initially choosing the long path and half choosing the short path.
Now consider that ants deposit pheromone at an approximately constant rate, travel at approximately the same speed, and travel in both directions between the nest and food source. As a result, after a given period of time, more ants have traversed the entire length of the short path than have traversed the length of the long path. This means that after the given period of time, the concentration of pheromone on the short path is higher than the concentration on the long path. A positive feedback process ensues, whereby after some time, most of the ants take the short path. Thus, the ants have collectively made a “decision”, and importantly, the decision is clearly the optimal one.
It is this kind of collective problem-solving behaviour described above that inspired the attempt to translate the essential features of biological ants onto artificial ants for use in computational problem solving, leading to the development of the Ant Colony Optimisation meta-heuristic [21].
The subsequent application of the Ant Colony Optimisation meta-heuristic to a communications network is quite a natural one to make. Table 1 lists the analogies made between real and artificial ants in the application of artificial ants to routing in communications networks; real ants become packets of information which physically travel through the network in a similar manner to regular packets. Pheromone concentrations on distinct trails translate to weightings for probabilistic link choice at network nodes. The deposition of pheromone then translates as incrementing the weights, and pheromone evaporation translates as decrementing the weights.
Analogies between biological and artificial ants
Biological Artificial Ants Information packets Trails Network links Trail intersections Network nodes Chemical pheromone Probabilistic weights on trail for link choice Pheromone deposition Weight increment Pheromone evaporation Weight decrement
Furthermore, from an engineering perspective, it is desirable to augment artificial ants with additional features not possessed by biological ants, in order to avoid certain shortcomings of biological ant systems.
For example, consider the double bridge experiment described above. The positive feedback that is seen to increasingly favour the selection of the shorter path, is essentially a transient effect, arising from the fact that the pheromone concentration increases at a faster rate on the short path. In the double bridge experiment it is also found that once a stable pheromone field is established on the short path, if a shorter path becomes available, then the ants are not always able to switch to it, and continue instead to travel on the same path [19]. This indicates that the positive feedback effect favouring the short path is strongly dependent upon the initial conditions, in this case, the initial absence of pheromone on either path.
This stagnation effect described above might be avoided if ants were somehow able to deposit pheromone in amounts that reflect the length of the path that they are travelling on. This would provide an additional mechanism for the differential reinforcement of the pheromone concentration on paths of different lengths, in a manner that would not be strongly dependent upon the initial conditions.
In designing an artificial ant-based algorithm, a differential reward mechanism can easily be introduced, whereby instead of depositing artificial “pheromone” at a constant rate, artificial ants deposit pheromone in quantities that are inversely proportional to the delay associated with the paths they travel on. This can be accomplished by programming the ants to effectively retrace their steps, and deposit pheromone after a path has been completed, and the path delay is known.
A number of algorithms that use ant-like agents have been proposed in the literature [8], [9], [10], [11] and [12]. These differ in their degree of sophistication, and in the details of their implementations. However, all have in common the idea of using mobile ant-like agents that autonomously traverse the network and try to find “good” routes between given origin-destination node pairs. The network information that is collected by the ants is then used to adaptively modify the network’s data traffic routing policy so as to exploit the best routes that are identified by the ants.
Ant-based routing algorithms can be characterised as follows. At each node of the network, an ant routing table is maintained. Such a routing table contains, for every possible destination node, a set of routing probabilities corresponding to each of the node’s outgoing links.
Ants are periodically created at every node and each ant is assigned to a given destination node. An ant departing from its origin node selects an outgoing link probabilistically, according to the routing probabilities contained in the ant routing table at the origin, and this process is repeated at each intermediate node until the destination node is reached. An ant stores in its memory the information about the route that it has taken, and the associated trip time. By re-tracing its chosen steps from the destination back to the origin, the ant is able to update the routing probabilities at the nodes that it visited. The updates are functions of the trip time measurements that were made by the ant on its original forward journey. The collective effect of these updates is intended to increase the probability that other ants select links that lie on routes with low associated trip times, and conversely, to decrease the probability of selecting links that lie on routes with large associated trip times. A positive feedback process therefore ensues, whereby the majority of ants travel on routes with low trip times, and links which lie on such routes have larger associated routing probabilities.
Simultaneously, a data traffic routing policy is specified as a function of the ant routing probabilities. The particular manner in which this is done varies from one ant-based algorithm to another, and depends on whether the network is connection-oriented or connectionless (see [1]). Ant-based algorithms that have been designed for connection-oriented networks [11] and [8] apply deterministic data routing policies, whereby connections are established by reserving spare capacity (if available) on links which have the highest associated ant routing probabilities. In contrast, ant-based algorithms that have been designed for connectionless networks [9] and [10] apply randomized data routing policies, whereby data packets are more likely to be routed on outgoing links which have the highest associated ant routing probabilities.
In both connection-oriented and connectionless networks, we see that the data traffic routing mechanism attempts to exploit the routes that are estimated by the ants to have a low associated delay.
We note that the role played by the ant routing probabilities in an ant-based routing algorithm is analogous to the role of the chemical pheromone in biological ant colonies. That is, the ant routing probabilities serve as a medium via which the ants can indirectly communicate and share information about the trip times associated with different routes.
An important feature that contributes to the ability of all ant-based algorithms to adapt to changes in the network environment, is that they perform some degree of exploration of the network.
In a biological ant colony, exploration occurs because ants are able to sometimes follow trails with lower pheromone concentration, or perhaps even travel in a direction in which the pheromone concentration is zero. The necessity for this type of behaviour in a biological ant colony is clear; for example, without exploration, ants would not have the means by which to discover new food sources when old ones are used up, or to find alternative paths between a nest and a food source if the original path is no longer viable.
In the network context, exploration can be characterized as the “probing” of a number of possible routes, in order to obtain information about them. Exploration is clearly a necessary feature for any routing algorithm that must “learn” about the network, because the algorithm must have some means for estimating or evaluating the delays associated with alternative routes, even if they are currently not in use.
Similarly, in a network in which the system parameters may change unpredictably, routes which initially have high associated delay, for example, may later have low associated delay. An exploration mechanism is therefore required, in order for an algorithm to be able to constantly probe and re-evaluate the delay associated with alternative routes.
In all of the ant-based routing algorithms proposed to date, exploration is achieved by constraining the ant routing probabilities away from zero, such that every outgoing link (and hence every possible route) has at least some small probability of being selected by an ant. In this paper, we demonstrate that network performance can suffer when exploration is performed in this manner, and we propose a modification to the design of ant-based routing algorithms which retains the ability to perform exploration without sacrificing performance.
The aim of this paper is to develop an analytical modelling approach for the study of ant-based routing algorithms that will permit us to gain insights into their fundamental properties. In order to do so, we restrict our attention to modelling a simple ant-based routing algorithm for connectionless networks.
The algorithm that we consider is based on AntNet [9], but contains only its fundamental features. This approach allows us to formulate an analytic model of the algorithm, presented in Section 5, that is both tractable and broadly representative of ant-based routing algorithms for connectionless networks. In particular, the insights gained using the analytic model and the improvements that we suggest in this paper apply to any routing algorithm that employs ant-like mobile agents.
Consider a network consisting of a set 
of nodes, connected by the set .gif){kind=small}
of directed links. We assume that .gif){kind=small}
is such that there is a path between any
two nodes. That is, the network is a connected graph. For each node .gif){kind=small}
, there are links to some subset of nodes
.gif){kind=small}
, which we call the neighbour nodes of
i.
At every node i, the following values are maintained for every destination node d in a “lookup table” format:
1. A set of Q-values,2
Qijd, for all neighbouring nodes .gif){kind=small}
, where Qijd
constitutes an estimate of the delay, or trip time, associated with travelling
from node i to d using the outgoing link
(i, j).
2. A set of ant routing probabilities 
ijd, for all neighbouring nodes .gif){kind=small}
, where ijd is the probability that an ant at
node i, with destination d, selects the outgoing link
(i, j).
3. A set of data routing probabilities ψijd, for
all neighbouring nodes .gif){kind=small}
, where ψijd is
the probability that a data packet at node i, with destination
d, is routed via the outgoing link
(i, j).
The ant and data routing probabilities are generated according to different functions of the trip times estimates, to be described shortly. Thus, ants and data packets share the same network, but are routed according to different “policies”. Furthermore, ants actively measure trip times and feed this information back into the routing tables by updating the trip time estimates, whereas data packets are passively routed through the network according to the data routing probabilities.
The behaviour and functionality of ants is as follows. Ants are regularly
created at all nodes and sent to all possible destination nodes. Each individual
ant is therefore assigned a particular origin-destination node pair. An ant with
origin node o and destination node d traverses the network by
randomly selecting an outgoing link at each visited node i according to
the ant routing probabilities ijd, until the destination node d is
reached. In particular, let ik,
k = 1, 2, … , N be the random
sequence of nodes visited by the ant, with
i1 = o and
iN = d, where N 
2 is a random variable denoting the number of nodes comprising
the ant’s trajectory.
The ant then retraces its trajectory by moving in the opposite direction from d to o. We consider the following two variants of the update method performed by the ant on its return journey.
1. The sub-path update method: The ant updates the trip time estimates at each of the nodes ik, k = 1, 2, … , N − 1, that it visited on the forward trajectory, according to the formula
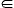(0, 1] is a damping, or stepsize parameter, which determines
the weighting of new information relative to the previous estimate when
computing the new estimate, and qik,ik+1,d
is the trip time measured by the ant in travelling from node
ik to d via the outgoing link
(ik, ik+1). This process
continues until the ant has returned to the origin node
i1 = o, whereupon it updates the value Qi1,i2,d
associated with the forward ant’s first hop link.
2. The single update method: The ant only updates the value Qi1,i2,d associated with its first hop link, according to the rule
The Q-value updating process is therefore driven by ants which travel from the origin to destination, possibly over a number of different routes, with each ant effectively performing trip time measurements on the network, and reporting the results back to the nodes at which the particular Q-values are maintained.
In general, the updating process specified by (1)
or (2)
would be carried out asynchronously for all Q-values .gif){kind=small}
, and for all destination nodes d. The
asynchronism arises from the fact that different ants experience different trip
times, in addition to the fact that there may not necessarily be network-wide
coordination of ant creation and despatch for different origin-destination node
pairs.
The key feedback mechanism between trip time estimation and routing lies in the update of ant and data routing probabilities. Each time a trip time estimate Qijd is updated, the corresponding ant and data routing probabilities are also updated. Following procedures that are similar to those proposed in [10] and [9], this is done according to the update rules
For values greater than or equal to 1, the parameter β acts as an “inverse temperature” parameter, which governs the degree of exploration carried out by the ants. As β increases, the link choice probabilities become more sharply “peaked” on the links for which the Q-values are smallest. The effect is that increasing the value of β results in a decrease to the level of exploration carried out by the ants.
Similarly, we see that σ controls the distribution of data traffic over the outgoing links, and thus governs the degree to which data traffic is distributed over multiple paths. By setting β < σ, we emulate the data routing mechanism employed in AntNet, whereby data packets have a higher probability than ants of selecting links with low associated delay. In this manner, data packets are biased towards the exploitation of links with low associated Q-values, whereas ants are biased towards network exploration, by virtue of the fact that they are more likely to select links with higher associated Q-values.
In this section, we develop an analytic model of the ant-based routing
algorithm described in Section 4.
Let the nodes in .gif){kind=small}
be labelled
i = 1, 2, … , S. For the analytic
model, we restrict our attention to a single destination node, labelled
S. In addition, we restrict the contents of the set .gif){kind=small}
to those links (i, j)
for which i ≠ S.
The model is posed as follows: let .gif){kind=small}
be a discrete iteration index. Following
the description of the routing algorithm in Section 4,
let 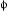ijS(β, n) be the probability
at iteration n of routing an ant currently at node i, whose
destination node is S, along the link (i, j), and let
ψijS(β, n) be the corresponding
routing probability for a data packet. Throughout the rest of the paper, we omit
the subscript S in the above quantities, since all quantities pertain to
the same destination node.
The ant routing probabilities are collected into the matrix Φ(β, n) of dimension (S − 1) × (S − 1), where
The routing probabilities 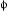iS(β, n) do not appear in the
matrix Φ(β, n), but can be obtained via the
relation
Similarly, the data routing probabilities are collected into the matrix Ψ(σ, n) of dimension (S − 1) × (S − 1). The routing matrices Φ(β, n) and Ψ(σ, n) uniquely determine the way in which the ant and data traffic is routed through the network.
Let .gif){kind=small}
be the rate of ant traffic entering the
network at node i, which is destined for node S, where .gif){kind=small}
. The values .gif){kind=small}
,
i = 1, … , S − 1, are collected
into the (S − 1)-dimensional vector .gif){kind=small}
. Similarly, let
si denote the data traffic demand entering the network
at node i, which is destined for node S, and let s be the
vector of data traffic demands.
The ant node flows, denoted .gif){kind=small}
, are given by a solution to the system of
equations
.gif){kind=small}
. The system of equations (7)
has a unique solution, provided that the matrix
Φ(β, n) is such that there exists a path of positive
probability from every node .gif){kind=small}
to the the destination node S [22],
in which case the matrix I − Φ(β, n)
is invertible and the solution can be written in vector form asThe data node flows, denoted wi(n) are given similarly by the solution to the system of equations
.gif){kind=small}
to the the destination node S, as
above. The resulting ant and data link flows are given
byThese are collected into the vector f(n), of dimension .gif){kind=small}
.
Next, we develop a model of the expected delays incurred by ants and data
packets as they traverse the network. We begin by considering the expected delay
on each link. Let Cij be the service rate associated
with link (i, j). The values Cij,
for .gif){kind=small}
, model the link capacities, which are
finite and strictly positive. The link flows and link capacities determine the
expected queueing delays associated with traversing network links. The expected
queueing delay associated with traversing the link (i, j), is
given by
Expression (11)
is the formula for the expected delay incurred by a packet in an
M/M/1 queue [23].
The use of (11)
therefore entails the assumption that the packet arrival process at link
(i, j) is a Poisson process, with arrival rate
fij(n), and that packet service times are
exponentially distributed with mean .gif){kind=small}
. This approximation is often employed to
model the stationary mean packet delay in queues within computer and
communications networks [1].
In particular, the function d(·, ·) increases monotonically as the
amount of traffic flow on the link increases, and tends to infinity as the
traffic flow approaches the link capacity, and is therefore suitable for the
basic purpose of introducing flow-dependent link delays into the analytic model.
Indeed, the exact form of d(·, ·) is not important for the purpose
of our model, provided d(·, ·) posesses the above (or similar)
properties. The total expected delay associated with traversing a link
(i, j) is given by
Let Qij(n) denote the expected delay incurred by an ant that travels from node i to the destination S, via the particular outgoing link (i, j), when the ant routing matrix is Φ(β, n), and the data routing matrix is Ψ(σ, n). We collect the Q-values into the vector Q(n), of dimension A. The Q-values are derived from the ant and data routing probabilities as follows.
Let Jj(n) denote the expected time taken by an ant to travel from node j to the destination node S, where the expectation is taken with respect to the current ant routing probabilities. Jj(n) is given by the solution to the system of equations
.gif){kind=small}
. The solution to the system of equations
(13)
can be written in vector form asThe Q-values are then given by
Note that in expression (13),
the summation over neighbouring nodes .gif){kind=small}
, is weighted by the ant routing
probabilities, Φ(β, n), rather than the data routing
probabilities, Ψ(σ, n). This is consistent with the
fact that it is the ant routing probabilities rather than the data routing
probabilities that govern an ant’s link selection.
We shall refer to the evaluation of Jj(n),
j = 1, … , S − 1, and
Qij(n) for all .gif){kind=small}
as Stage 1 of the analytic model.
Stage 2 of the analytic model involves the generation of the new ant and
data routing matrices, Φ(β, n + 1) and
Ψ(σ, n + 1), respectively. Following the
description of the routing algorithm given in Section 4,
the ant routing probabilities are updated according to
Expression (18),
and consequently also expression (17),
are not defined in the event that for a given node i, the values
Qik(n) for all .gif){kind=small}
are not finite. Such a situation occurs
if fij 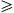Cij for all .gif){kind=small}
. In order for the analytic model to be
well-defined under these circumstances, we arbitrarily set .gif){kind=small}
, where .gif){kind=small}
.
The data routing probabilities are updated according to
As before, in the event that the values
Qik(n) for all .gif){kind=small}
are not finite, we arbitrarily set .gif){kind=small}
.
We can express the analytic model using a more compact notation, as follows.
Consider the (S − 1) × 2(S − 1)
matrix
Π(n) = (Φ(β, n), Ψ(σ, n)),
and define the mapping .gif){kind=small}
, given by
maps ant routing probabilities and link delays to expected ant
delays, J(n). Define a mapping .gif){kind=small}
, given by.gif){kind=small}
are given by (18)
and (20),
respectively. Ω maps Q-values to ant and data routing probabilities. We
note that for finite values of β and σ, it is not possible to
simultaneously have .gif){kind=small}
and .gif){kind=small}
, or vice versa. Therefore, these
possibilities do not need to be considered in the definition of Ω.
We can express the analytic model as an iteration of Q-values
It is clear that the mapping .gif){kind=small}
is well defined at every iteration .gif){kind=small}
, in the sense that the matrices
I − Φ(β, n) and
I − Φ(σ, n) are invertible, provided
that the initial values Q(0) are strictly positive and finite. The same
is true of the mapping .gif){kind=small}
, provided that the initial ant and data
routing matrices Φ(β, 0) and
Φ(σ, n) each specify at least one path of positive
probability from every node .gif){kind=small}
to the destination node S [22].
In general, the mappings given in (23)
and (24)
are not continuous, due to lack of continuity of the mapping Ω as .gif){kind=small}
. It is therefore not possible to
guarantee that the analytic model has a fixed point under general circumstances.
However, in our numerical experience, we have always been able to solve (23)
and (24).
Furthermore, Ω is a continuous mapping for a special case that is
characterized by light traffic demands, where
fij < Cij for all
links .gif){kind=small}
under all possible routing policies
Φ and Ψ. This special case arises in the analysis of the model
presented in Section 6.
We note that the ant-based routing algorithm described in Section 4 is inherently decentralized and distributed. As a result, the updates of the routing probabilities and Q-values occur concurrently and asynchronously, without “global” network-wide coordination. In contrast, the formulation of the analytic model entails an approximation to the real ant-based routing algorithm, known as a time-scale separation approximation. In particular, the analytic model calculates all expected network delays exactly at each iteration, prior to a routing update at the subsequent iteration. Despite this approximation, we find that we can use the analytic model to gain some important insights into the equilibrium behaviour of the ant-based routing algorithm.
In this section, we provide an overview of our approach to the analysis of the ant-based routing algorithm described in Section 4. In particular, we comment on the scope of the analytic model that was presented above, and the nature of the information that will be gained through its analysis.
We begin by noting that the routing algorithm described in Section 4 must perform two important tasks. The first task involves the updating of Q-values, using the trip times experienced by ants. This can be regarded as an “information gathering” activity, where the information to be gathered regards the network trip times and delays. The second task involves the use of the information contained in the Q-values, in order to construct a data routing policy.
In Section 6, we focus on the first task, that is, the “information gathering” properties of the algorithm. In order to do this, we consider the behaviour of the agents in the absence of data traffic demands. We assume that the load placed on the network by ant traffic is negligible, so that ants experience only a fixed transmission delay on each link that is traversed, but no flow-dependent queueing delays. The resulting optimisation problem is a static shortest path problem on the network, which provides a simple context in which to investigate some fundamental aspects of the ant-based algorithm. In particular, we use this context to highlight the fact that ant-based routing algorithms employ the same policy for exploration of the network as they do for decision-making, which can lead to sub-optimal routing decisions. We propose a simple modification to the ant exploration mechanism which eliminates this type of error.
In Section 7, we consider the second task of routing in the presence of data traffic demands. In this context, we are able to study the ability of the algorithm to perform load-balancing of data traffic over multiple paths for given origin-destination node pairs. Importantly, there do not exist static shortest paths as a point of reference, because the expected delay associated with each path is dependent upon the data traffic flow on the path, and hence dependent upon the current data routing policy.
The appropriate points of reference for an equilibrium analysis of the algorithm are the system and user optimal traffic flows. We demonstrate that there are a number of inefficiencies associated with the ant-based algorithm with respect to such measures, and we propose modifications to the exploration and load-balancing mechanisms which eliminate these inefficiencies.
In this section, we analyse the ant-based algorithm in the absence of data
traffic demands, so that at all iterations .gif){kind=small}
, we have .gif){kind=small}
for all links (i, j).
Furthermore, we assume that the load placed on the network by the ants is
negligible, that is .gif){kind=small}
, for all links (i, j).
The link delays can then be approximated by constant values .gif){kind=small}
, which do not depend on the ant or data
routing matrices, and hence do not depend on the iteration index n.
In this scenario, the network optimisation problem reduces to a deterministic shortest path problem, where the objective is for the ants to identify a shortest path from each node to the destination node S. In particular, we can gain insight into the effect that the exploration mechanism employed by the ants has on their ability to perform this task.
As a point of reference, we consider the set of “optimal Q-values” [24] and [2] for the deterministic shortest path problem, given by
.gif){kind=small}
,
j = 1, … , S − 1, are the
(optimal) shortest path costs [25]
associated with reaching the destination node S from node j (with
.gif){kind=small}
). A shortest path from any node to
S can then be constructed by simply selecting at each node i the
outgoing link which satisfies .gif){kind=small}
until the destination node S is
reached.
It is shown in [22]
that the mapping (24)
is continuous3
for the special case where the link delays are constant, and therefore has a
fixed point [26].
Furthermore, any such fixed point .gif){kind=small}
has a corresponding set of
Q-values which satisfy
Indeed, the result (25) is not altogether surprising, given that the ant routing probabilities updated according to (17) constitute a non-degenerate randomized policy with all positive probabilities, whereas it is well-known that an optimal policy for the shortest path problem is deterministic [25]. In terms of the ant behaviour, we see that while some fraction of ants travel on the shortest paths, the remaining ants travel on sub-optimal paths. The mean trip time experienced by ants travelling between a given origin and destination node pair must therefore be greater than the shortest possible trip time between the nodes.
Importantly, it is not always possible to construct a shortest path from any
node to the destination S by simply selecting at each node i the
outgoing link which satisfies arg .gif){kind=small}
. Examples of this failure to identify
shortest paths based on the Q-values generated by the ants are shown
using both the analytic model and simulation experiments presented in [22].
This type of failure can be understood by observing that the shortest path
problem can be cast as a Markov decision problem [25];
it can be shown that the randomization present in the ant routing policy
effectively modifies the Markov decision problem that the ants are
attempting to solve, and under certain circumstances (see [22]),
the modified problem has an optimal policy that is different to the optimal
policy for the original shortest path problem.
This demonstrates a fundamental problem associated with the exploration mechanism that is employed by ant-based routing algorithms; that the ants employ the same policy for exploration as they do for decision-making, or stated another way, that there is no separation between the mechanism used for exploration of alternative routes and the mechanism used to exploit routes which are estimated to be optimal. In the reinforcement learning literature, such a learning algorithm is often referred to as being “on-policy” [24] and [2]. In contrast, a learning algorithm which possesses a complete separation between its exploration and decision-making mechanisms is referred to as being “off-policy” [24] and [2]. In the language of control theory [27], we see that the dual tasks of system identification and control are coupled, and that there is a tradeoff between these tasks.
Much of the literature describing ant-based routing algorithms appears to suggest that this tradeoff between exploration and exploitation cannot be resolved, or that this coupling is not problematic. We argue that this is not the case, and we present a simple modification which can be made to the exploration mechanism employed by the ants, which results in the complete separation of exploration and exploitation, thus rendering it an off-policy learning algorithm.
Specifically, it is sufficient to restrict ant exploration to the selection
of its first link when leaving the origin node, and subsequent links are
selected according to the update rule (17)
in the limit as β → ∞. This corresponds to zero exploration
probability for ant routing decisions at all stages of the forward path, except
for the ant’s first hop, when all outgoing links have a positive probability of
being selected. It is shown in [22]
that this modification to the analytic model results in a fixed point .gif){kind=small}
which constitutes an optimal solution to
the shortest path problem, that is, the corresponding Q-values
satisfy
In Section 7, we demonstrate that when data traffic demands are placed on the network, the on-policy property of ant-based routing algorithms leads to inefficiency in the load-balancing of data traffic, and that an off-policy version of the ant-based algorithm is desirable in this more typical scenario as well.
In this section, we investigate the behaviour of the ant-based routing algorithm in the presence of data traffic demands. Furthermore, we include in our analysis the effects of the ant traffic demands and ant traffic flows, because when the data traffic demands are high, the presence of a small amount of additional traffic due to the ants, can have a non-negligible effect on the the queueing delays.
In contrast to the constant link delays in Section 6, the presence of data traffic flows results in link delays that are dependent upon the total amount of traffic that is carried on the links. The flow-dependent link delays arise as a result of the buffering and processing of packets awaiting transmission on the links, which have finite transmission capacities. This introduces a strong coupling between the traffic routing policy, and the delays that are experienced by packets on each link, and the interaction of a traffic stream with the network is therefore an important consideration.
Furthermore, the interaction of different traffic streams with each other is also an important consideration, given that multiple traffic streams can effectively “compete” for finite shared resources, comprised by the packet buffers and transmission capacity. This adds complexity to the evaluation of a given routing policy; the optimisation scenario is no longer a simple (static) shortest path problem, as discussed in Section 6. For example, a particular routing policy may be beneficial to one traffic stream but detrimental to another, according to some performance measure, such as delay per unit of traffic transmitted. This leads to the notion of “users”, and user-equilibria or user-optima. Alternatively, an average system-wide performance measure can be used to evaluate a given routing policy, thus leading to the notion of a system optimum.
Ant-based routing algorithms such as AntNet were not designed with any specific equilibrium concept in mind, but rather as “best-effort” type routing algorithms [9] and [1]. Analysis of ant-based algorithms has been carried out almost exclusively via simulation experiments which focus on transient measures of performance and recovery in response to network changes. AntNet has been reported to perform very well against such measures [9].
Although the adaptive transient properties of ant-based routing algorithms are extremely important, the authors believe that the equilibrium behaviour of these algorithms is also an important consideration. In particular, in addition to possessing the ability to react rapidly to network changes, an ant-based routing algorithm should also converge to “efficient” equilibrium routing policies during the (perhaps short) periods in which the network conditions do not change significantly.
In this section, we demonstrate that the current design of ant-based routing algorithms leads to certain inefficiencies with respect to equilibrium delay-based measures, and we suggest improvements to their design which improve their performance, without compromising their desirable transient adaptive properties. We begin by giving a brief overview of equilibrium traffic optimisation concepts.
The analysis of traffic equilibria on networks originated with the work of Wardrop [17], which developed a means for analysing and characterizing vehicle traffic flows on road networks. Wardrop’s First Principle can be stated equivalently in the following three ways:
or“The travel times on all used paths between an origin and a destination point are equal, and less than those which would be experienced by a single vehicle on any unused path”
or“No traveler can improve his travel time by unilaterally changing routes”
“Every traveler follows the minimum travel time path”.
If we replace “traveler” and “vehicle” with “packet” in the above definitions, we obtain the appropriate definition for a Wardrop equilibrium in a packet-based communications network. In particular, a data traffic routing policy Ψ corresponds to a Wardrop equilibrium if no packet can unilaterally decrease its trip time from its origin to the destination by following a policy that is different to Ψ.
The Wardrop equilibrium was later shown to be a special case of the Nash equilibrium [28], thus establishing a connection between the study of traffic equilibria on networks and game theory [15]. This connection has since been used extensively in the analysis and characterization of network routing algorithms and their equilibrium properties (see for example [29], [30] and [31]).
Nash and Wardrop equilibria are examples of user equilibria [28], which arise in the network context when a number of users compete for a set of shared finite resources. In the communications network context, shared resources correspond to finite-capacity links. A user can be considered to be a traffic stream, or traffic demand, and each user is therefore associated with a given origin-destination node pair.
Wardrop equilibria arise as examples of Nash equilibria in the limit as the total number of users becomes infinitely large, but where each individual user has a negligible impact on the delays experienced by other users [32]. In the context of a packet-based connection-less communications network considered here, the physical interpretation of this limit is one in which the users correspond to individual packets.
In general, user equilibria are characterized by the “selfish” behaviour of the users. That is, each user makes routing decisions in an effort to reduce its own incurred cost (per unit of traffic routed), without taking into consideration the effect that its own decisions may have on the costs incurred by other users. For this reason, user equilibria are sometimes referred to as competitive, or non-cooperative equilibria [30] and [31].
In contrast, a system optimum is achieved when the total average packet delay is minimized over the set of all possible routing decisions, and is characterized by the condition that all routes between an origin and a destination node that are actually used have equal marginal delay, which is less than the marginal delay associated with all alternative unused routes [1].4
The fact that ant-based routing algorithms update the Q-values and routing probabilities based on ant trip time measurements rather than marginal delay measurements, suggests that it is unlikely that ant-based routing algorithms would, in general, achieve routing policies that correspond to a system optimum. Indeed, algorithms such as AntNet do not lay claim to the goal of system optimal routing [9], and are proposed by their authors as an alternative to the shortest path routing algorithms that are widely used in modern communications networks [1] and [14].
Furthermore, we do not expect that ant-based routing algorithms should have the ability to systematically attain general user (Nash) equilibria due to the “stateless” [1] nature of the data traffic routing, whereby nodes differentiate incoming data packets according only to their destination node, and not according to their node of origin or prior “history”. Specifically, since all packets arriving at a node that have the same destination are routed according to a common set of routing probabilities, then no node can be acting exclusively on behalf of any user or subset of users.
Indeed, algorithms that are designed to attain Nash equilibria allow each user to control the flow of their own traffic at every node that is accessible to the user. This is usually achieved by allocating to each user a finite set of paths, and allowing the user to make routing decisions in response to the decisions made by other users [30] and [31]. Clearly, this type of control lies beyond the scope of ant-based routing algorithms (without major modifications) and other stateless routing algorithms.
Despite the fact that system optimal and Nash equilibrium routing are (in general) beyond the scope of what is attainable by a stateless routing algorithm, it is significant that Wardrop equilibria are not incompatible with stateless routing. Specifically, in Section 8 we develop an off-policy version of the ant-based routing algorithm that is able to achieve Wardrop equilibria.
In this section, we use the analytic model to investigate some of the properties of the ant-based routing algorithm in the presence of data traffic demands. For each case that we investigate, we compare our results with those obtained from simulation experiments. We begin by providing a brief description of the simulation model and the methods used to compare the simulation output with the analytic model.
The simulation model consists of a packet-level discrete-event simulator, which was designed to reflect the features of the ant-based algorithm and of the network which are captured in the analytic model. The main features of the simulation model are as follows.
There is a single destination node, labelled S, and data packets are
created as a Poisson stream between the origin-destination node pairs
(i, S), for
i = 1, … , S − 1, at fixed
rates given by si 0. Ant packets are created as a Poisson stream between the
origin-destination node pairs (i, S), for
i = 1, … , S − 1, at fixed
rates given by .gif){kind=small}
, where .gif){kind=small}
is the number of neighbour nodes of node
i, and k > 0 is a parameter which governs the rate of
emission of ants relative to the emission of data packets. For the simulations
presented in this section, we set k = 0.01. The reason for this
is to make the ant traffic load small compared to the data traffic load, as
intended in previous simulation studies of ant-based routing algorithms such as
[9].
Ants and data packets behave as described in Section 4.
For reasons to be discussed in the following section, ants employ the single
update method, and there is no mechanism to prevent ants or data packets
from performing loops. All packets (including ants) arriving at the link
(i, j), are placed in a single-server FIFO queue [23],
where the service times are exponentially distributed with mean .gif){kind=small}
. Once a packet leaves the queue, it
experiences a fixed link transmission delay rij. The
total delay experienced by a packet on a link is given by the sum of the random
amount of time spent in the queue (including service time), and the
deterministic link transmission delay.
Updates of the ant and data routing probabilities at a given node i,
are triggered whenever an update to a Q-value,
Qij, for .gif){kind=small}
occurs. The ant and data routing updates
are carried out according to Figs. (3)
and (4).
The simulation model is thus comprised of a network of M/M/1 queues, with Poisson traffic sources originating at the nodes. The simulation model was validated by comparing the mean packet delay estimates in the network with their known mathematical expectations under fixed routing policies. To validate the mechanisms for updating the routing policy, the simulation model was compared against known test cases.
Data from the simulation model is collected as follows. By sampling
Qij, .gif){kind=small}
, at regular simulation time intervals, we
construct a time series for each Q-value. The equilibrium value of
Qij is estimated by taking the average of the
corresponding time series once the system has reached equilibrium. For each
example described in this paper, we produce 10 replications to obtain the
equilibrium estimates .gif){kind=small}
, as well as the associated 95%
confidence intervals. These can be used to compare the equilibrium behaviour of
the simulation model with the fixed point of the analytic model.
We consider first the standard case of operation of the ant-based routing algorithm where the parameters β and σ are finite and greater than unity. Recall that β parameterizes the degree of exploration that is carried out by the ants and σ, governs the degree to which data traffic is routed over multiple paths. Setting σ < ∞ allows for some fraction of the data traffic to be routed on links which do not have minimum associated Q-values, thus effectively “spreading” the traffic demand over alternative paths, and ideally, resulting in a certain degree of load balancing of data traffic.
Typically, one would choose β < σ, so that in comparison to the ant routing probabilities, the data routing probabilities would be more sharply “peaked” at the outgoing links with minimum associated Q-values. The reasoning behind such a scheme is that ants should, relatively speaking, have a greater propensity for exploration, whereas data packets should have a greater propensity for the exploitation of the paths with lower estimated delay. Indeed, this is one of the strategies employed by the AntNet algorithm [9].
Consider the four-node network shown in Fig.
1. Let Cij = 10 and
rij = 0.1, for all .gif){kind=small}
. The destination node is
S = 4. We begin by investigating an example where the traffic
load is light, with data traffic demand vector
s = (5, 5, 0, 0). The rate of ant traffic
entering the network is given by .gif){kind=small}
, so that .gif){kind=small}
, with k = 0.01.
Fig. 1. Four node network. The destination is node 4.
Let β = 2, σ = 4, with the initial
condition Qij(0) = 1 for all .gif){kind=small}
. For the analytic model, we implement the
following damped version of iteration (23):
(0,1] is a damping parameter. The value of the damping parameter
has no effect on the fixed points obtained from the analytic model, and serves
simply to produce “smooth” trajectories with transient behaviour that closely
resembles that of the real system.
The trajectories of the Q-values obtained from the numerical iteration
of the analytic model are shown in Fig.
2. There are eight individual trajectories, corresponding to the
Q-values for .gif){kind=small}
, excluding those for which
i = S = 4. The corresponding simulated
trajectories, generated by using the single update method (see Section 4),
are shown in Fig.
3. Each trajectory is obtained by taking the “pointwise” average over 10
independent simulations.
Fig. 2. Q-value trajectories obtained from iteration of the analytic model (27).
(23K)
Fig. 3. Q-value trajectories obtained via simulation of the ant-based routing algorithm using the single update method.
Comparing Fig. 2 and Fig. 3, we see that the analytic model captures several of the qualitative features of the simulated trajectories. Despite the time-scale separation approximation, we observe that the trajectory produced by our model is able to capture the transient behaviour of the simulation model for this example.
Of greatest interest are the equilibrium Q-values, which are
summarized in Table
2. The first column of Table
2 contains the indices .gif){kind=small}
. The second column contains the entries
of the vector .gif){kind=small}
, which is the fixed point obtained using
the analytic model. The third column contains the 95% confidence intervals for
the equilibrium values, .gif){kind=small}
, obtained using the simulation model with
the single update method. The quantities .gif){kind=small}
are calculated as described in Section 7.2.1.
It is seen in Table
2, that all of the entries of .gif){kind=small}
lie within the respective 95% confidence
intervals for .gif){kind=small}
.
Light traffic load example with data traffic demand vector s = (5, 5, 0, 0)
It is interesting to note that in many experiments, we found there to be
differences between the confidence intervals for the equilibrium Q-values
obtained from simulation experiments using the subpath and single update
methods, respectively [22].
This difference can be attributed to a statistical bias associated with the
sub-path update method, which arises from the fact that some ants perform loops,
and thus re-visit one or more nodes on their forward path. The trip times
recorded from each revisited node to the destination are therefore correlated,
since the trip time measurement associated with the first visit to a node is
necessarily greater than the trip time measurement associated with the
subsequent visit, and so forth for each re-visit. This correlation introduces a
statistical bias with respect to the Q-values, .gif){kind=small}
, generated by the analytic model, which
are the mathematical expectations for the trip times associated with reaching
node S via each of the links in .gif){kind=small}
. The nature of this bias is discussed in
more detail with examples in [22],
and follows an analysis of correlated trajectories in Monte Carlo methods for
reinforcement learning, as discussed in [1].
In this paper, we employ the single update method in the simulation model.
We note that ant-based routing algorithms typically employ the sub-path update method, as this makes more efficient use of the information collected by each ant and leads to a faster rate of convergence. If the sub-path update method is used, then ant-based routing algorithms typically also include measures to counteract the type of trip time sampling bias described above, the most common being a looping-prevention mechanism (see, for example, [9]). We have chosen not to model a looping-prevention mechanism in our analytic model, as this would render the analytic model intractable, and would not provide any additional insight into the equilibrium behaviour of the system, which is the primary goal of this paper.
The fourth and fifth columns of Table
2 show the values of the ant and data routing probabilities at the fixed
point, denoted .gif){kind=small}
and .gif){kind=small}
, respectively. As expected, given the
choices of β = 2 < σ = 4, the
data routing probabilities are more sharply “peaked” on links with the smallest
associated Q-values. Consider, for example, the Q-values .gif){kind=small}
. Both ants and data have a greater
probability of selecting the link (1, 3), that is, .gif){kind=small}
and .gif){kind=small}
, but this probability is greater for the
data than the ants, that is, .gif){kind=small}
.
The sixth column of Table
2 contains the entries of the expected data traffic flow vector,
fdata, produced by the routing matrix .gif){kind=small}
. We can compare fdata
with the flow vectors fsys and fwar, which
contain the link flows associated with a system optimum and Wardrop equilibrium
for this problem. These are shown in the last two columns of Table
2, respectively.
By inspection, we see that the equilibrium flows achieved by the analytic
model do not correspond to either a system optimum or a Wardrop equilibrium. The
same can be reliably inferred for the flows produced by the simulation model,
since from Table
2, we see that .gif){kind=small}
, and the steady-state flow of traffic
entering each link is strongly coupled to the Q-values via the routing
probabilities (and is subject only to stochastic fluctuations resulting from the
randomized nature of the packet routing). Computationally, we can compare
fdata against the flow vectors fsys and
fwar, with respect to system-based and user-based performance
measures, as follows.
The system performance measure that we consider for a given flow vector, f, is the total average packet delay, given by
Performance measures for light traffic load example
fsys fwar fdata Utotal(f) 4.41 4.42 4.68 0.55 0.54 0.56 0.33 0.34 0.38
The packet (user) performance measures associated with a given flow vector are specific to each individual o–d pair. For a given o–d pair (i, 4), the packet performance measure associated with a given routing matrix Ψ and flow vector fdata, is the expected delay incurred by a single data packet travelling from i to 4, given by the ith entry of the vector.
.gif){kind=small}
and .gif){kind=small}
, for each of the flows
fsys, fwar, and fdata. We
see thatSimilar results are observed when the traffic load on the network is higher.
Consider the same example, but with the data traffic demand vector
s = (10, 2, 0, 0). The results are summarized in
Table
4, where it is seen that all entries of .gif){kind=small}
lie within the 95% confidence intervals
for .gif){kind=small}
.
Heavier traffic load example with data traffic demand vector s = (10, 2, 0, 0)
As before, we can compare fdata against the flow vectors fsys and fwar, with respect to system-based and user-based performance measures. This comparison is shown in Table 5.
Performance measures for heavier traffic load example
fsys fwar fdata Utotal(f) 7.31 7.41 7.71 0.66 0.66 0.68 0.37 0.38 0.40
In summary, the calculations shown in Table 3 and Table 5 for the light and heavy traffic load examples, respectively, demonstrate that the data traffic flows produced by the analytic model and the ant-based routing algorithm are sub-optimal with respect to both system and user performance measures.
In general, these inefficiencies arise because the ant-based routing algorithm possesses only a limited ability to balance traffic load in a way that is specific to the conditions encountered on the outgoing links at each network node. For example, we saw in the example summarized in Table 2, that even though traffic is assigned to outgoing links in a manner that reflects the relative magnitudes of the associated Q-values, the use of a finite value of σ means that it is impossible to set the traffic flow to zero on certain links, or conversely, to send all traffic exclusively on a single outgoing link, if this happens to be more efficient from a system or user point of view.
Of course, a “naive” although very common [14] approach towards the elimination of the above inefficiencies (including loops), would be to let data packets exclusively follow links that are estimated by the ants to lie on paths of least cost. This would amount to a form of shortest path routing [1], which, as we shall discuss in Section 7.2.3, has its own set of associated problems, the most notable of which are oscillatory routing policies, and the inability to perform effective load balancing when the traffic demands are high.
This raises the question of how an ant-based routing algorithm could provide effective load-balancing, while also exploiting paths with low associated delay, in order to eliminate inefficiencies in the data routing policy. We address this issue in Section 8.
Increasing the value of the load-balancing parameter σ reduces the amount of data traffic that travels on very high delay routes. The ultimate outcome of this occurs if we let σ → ∞. In this limit, we see from (4), that data traffic would be routed exclusively on links with minimum associated Q-values. We note that such a data routing mechanism corresponds to shortest path routing [1], but due to equation (19), allows for equal sharing if multiple paths have the same estimated delay.
Shortest path routing of data traffic is a feasible option when the traffic load on the network is light. However, under heavy traffic load conditions, it is well-known that adaptive shortest path routing can lead to certain links becoming overloaded, leading to undesirable oscillations in the routing policy [1] and [37]. Indeed, we have observed similar instabilities in our analytic and simulation models when σ is set to a large value [22].
In this regard, the heuristic data routing mechanism employed by the ant-based routing algorithm is more robust than shortest path data routing, when the traffic load placed on the network is high. We note that in the simulation experiments carried out in [9], AntNet was found to perform better than competing algorithms, precisely because of the inherent load balancing ability that is provided by the use of randomized data routing policies. The routing algorithms that AntNet was compared to in [9], included OSPF [14], Distributed Bellman–Ford [1], Q-Routing [3], and PQ-Routing [4]. All of these employed shortest path (as opposed to multipath) routing for data traffic, and therefore lacked the ability to effectively perform load balancing. This was one of the primary reasons for which the above algorithms were found to compare poorly against AntNet in many situations.
The analysis presented in Sections Sections 6 and 7 suggests that the efficiency of ant-based routing algorithms can be improved by making a number of modifications to their basic operation, which we describe in this section. Specifically, we observed in Section 6 that ant-based routing algorithms are on-policy learning algorithms [24] and [2], which means that ants use the same policy for exploration as they use for “decision-making”. This can result in a failure to correctly identify shortest paths in the context where the link costs are fixed.
In the presence of data traffic demands, the link delays depend upon the amount of data traffic that is carried on them, and as such, there do not exist static shortest paths on the network. However, analogous problems arise when the link delays are flow-dependent. Specifically, the on-policy nature of ant-based routing algorithms entails the property that ants use the same policy, Φ, to perform the task of exploring new routes as well as to estimate the trip times experienced by data packets. This is undesirable for the following reasons:
1. Since ants and data packets are routed according to different policies (Φ and Ψ, respectively), the distribution of trip times experienced by ants is different to that for trip times experienced by data packets, and the corresponding means are different in general. As a result, the Q-values, which are based on ant trip time measurements, are in fact “perturbed” with respect to the delays experienced by data packets. Consequently, data routing decisions are based upon these perturbed estimates, rather than estimates of the actual data traffic delays.
2. There is an inherent coupling between the tasks of ant routing, network exploration, and data routing (which includes the task of load-balancing), and as a result, the perturbation described in (1) affects all of these tasks simultaneously.
3. The perturbation and coupling described above lead to inefficient data routing with respect to user and system-based equilibrium performance measures, as demonstrated in Section 7.
Although ant-based routing algorithms attain a certain degree of differentiation between the tasks of data routing and network exploration (for example, by setting β < σ < ∞), we see that this coupling cannot be eliminated without making some fundamental changes to the way in which these tasks are carried out.
The above considerations motivate our proposal of an off-policy version of the ant-based routing algorithm, which is designed to eliminate the sources of inefficiency that we have identified. The modifications we propose achieve a complete separation between the tasks of network exploration and delay estimation, while maintaining the attractive properties of ant-based routing algorithms.
An off-policy version of the algorithm can be achieved as follows. As described in Section 6, ant exploration can be maintained by allowing ants to perform exploration only on their first hop. For subsequent decisions, ants follow the current data routing policy, Ψ. The result is that the ant trip times, and hence the Q-values, reflect the delays incurred by data packets. In particular, the value Qij constitutes an estimate of the delay that would be incurred by a data packet at node i, if it were to select the outgoing link (i, j), under the current data routing policy, Ψ. This contrasts with the original on-policy version of the ant based algorithm, in which ants and data use different routing policies, so that the “representation” of the network delays, comprised by the Q-values, does not accurately reflect the data traffic delays.
Furthermore, by restricting ant exploration to the first hop, we are able to decouple the exploration mechanism from the data routing policy Ψ. The off-policy version of the algorithm therefore only requires a single routing policy Ψ for both ants and data packets, as well as a first hop exploration mechanism for the ants. Indeed, any exploration mechanism which assigns a non-zero probability to each link when choosing an ant’s first hop is, in principle, sufficient [24] and [2].
In addition, we propose an alternative update mechanism for the data routing matrix Ψ, which does not constrain the data routing probabilities away from the values 0 and 1. The mechanism that we present is adapted from one employed in [36], where we have replaced the marginal delay estimates in [36], with the Q-values used by the ant-based routing algorithm.
Instead of updating the data routing matrix according to the rule (4),
the updates are performed as follows. Suppose a Q-value at node i
is updated by an ant. At this given point in time, let .gif){kind=small}
be the subset of links .gif){kind=small}
for which
The data routing probabilities are then updated according to the rule
We see from (31)
that this update procedure increments the amount of data traffic that is routed
on links with minimum associated Q-values, and decrements the amount of
data traffic that is routed on all other links. From (29),
we see that the magnitudes of the increments and decrements is governed by the
amount by which the Q-values deviate from the minimum Q-values, .gif){kind=small}
, as well as the magnitude of the flow
deviation parameter λ.
The presence of the term .gif){kind=small}
in the denominator on the right-hand side
of (29),
serves to scale the size of the increments and decrements so that they remain
consistent with the order of magnitude of the current Q-values. The
update procedure (31)
preserves the normalization of the routing probabilities, and the min{·, ·}
operation in (29)
prevents the routing probabilities from ever becoming negative.
It should be noted that the data routing update procedure given by expressions Figs. (28), (29), (30) and (31), does not prevent any given data routing probability, ψij, from becoming equal to zero (or from remaining equal to zero if so initialized). In this case, sufficient exploration of alternative routes is maintained by the ant first hop exploration mechanism.
The analytic model presented in Section 5 can be straightforwardly adapted to represent the off-policy version of the ant-based routing algorithm. This is described in Appendix A, where we show that the analytic model for the off-policy algorithm can be expressed as an iteration of data routing probabilities
The mapping (32)
is iterated for the four node network network shown in Fig.
1, with Cij = 10 and
rij = 0.1, for all .gif){kind=small}
, and data traffic demand vector
s = (2, 10, 5, 0). The ant traffic demands are
again given by .gif){kind=small}
, with .gif){kind=small}
and k = 0.01. The
stepsize and flow deviation parameters are set to γ = 0.01 and
λ = 0.001, respectively. The analytic and simulation results
are summarized in Table
6, where it is seen that the entries of .gif){kind=small}
fall within the 95% confidence intervals
for .gif){kind=small}
. We note that for this and the following
experiments, we adapted the simulation model described in Section 7.2.1
to implement the off-policy modifications.
Results for the off-policy algorithm
Recall the definition of a Wardrop equilibrium given in Section 7.1. It stipulates that a routing matrix Ψ corresponds to a Wardrop equilibrium if, for all origin-destination node pairs, the paths which carry (strictly) positive data flow have the minimum delay under Ψ, and all unused paths (which carry zero data flow) have a delay which is greater than or equal to the minimum delay under Ψ.
From Table 6, we see that the data traffic flows at the fixed point, fdata, are the same as the Wardrop equilibrium flows fwar. We can verify that fdata corresponds to a Wardrop equilibrium by considering the delays associated with paths in the network.
In order to calculate the path delays for this example, we use the link
delays, Rdata, which are shown in the last column of Table
6. Consider, for example, the o–d pair (1, 4). One
possible path between node 1 and node 4 is {1, 3, 4}. The total delay
on this path is given by .gif){kind=small}
. This path carries a positive data flow,
because .gif){kind=small}
and .gif){kind=small}
are both positive. Repeating this
procedure, the total delay and flow status of all paths in the network can be
determined, as shown in Table
7 (excluding those which contain loops, since there is an infinite number of
such paths, and we can see from Table
7, that all such paths carry zero flow).
Path delays for the example summarized in Table 6
o–d pair Path Total delay Flow (1, 4) {1, 2, 4} 1.11 No {1, 3, 4} 0.92 Yes {1, 2, 3, 4} 1.11 No {1, 3, 2, 4} 1.33 No (2, 4) {2, 4} 0.91 Yes {2, 3, 4} 0.91 Yes {2, 1, 3, 4} 1.12 No (3, 4) {3, 4} 0.70 Yes {3, 2, 4} 1.11 No {3, 1, 2, 4} 1.31 No
The paths which carry positive data flow, indicated by a “yes” in the last
column of Table
7, have smaller delays than all other (unused) paths. Therefore, the routing
matrix .gif){kind=small}
produces a Wardrop equilibrium.
We conclude this section by considering an example of a larger network, shown in Fig. 4. The network has 24 nodes and 72 links, and is based on the GEANT network, a pan-European data communications network for research and education. The link capacities are indicated in Fig. 4, and the link transmission delays are determined by geographical distance. For the experiment, we let the destination be node S = 24, and we let the data traffic demand vector be
Fig. 4. Twenty-four node network. The destination is node 24.
The ant traffic demands are given by .gif){kind=small}
,
i = 1, … S − 1, with .gif){kind=small}
and k = 0.01. As for the
smaller network examples, we found that all of the entries of the fixed point
vector .gif){kind=small}
fall within the corresponding 95%
confidence intervals for .gif){kind=small}
, a selection of which are shown in Table
8 (we do not show the Q-values associated with all links due to space
limitations). We also observe that the link flows produced by the analytic model
of the off-policy algorithm coincide with Wardrop equilibrium flows.
Selected results for the off-policy algorithm: 24 node network
It turns out that the Wardrop equilibrium property observed in the above examples is in fact a general property of any fixed point of the iteration (32), as stated in Theorem 1 below.
Let .gif){kind=small}
be the set of all routing matrices Ψ[0,1](S-1)2, for which the
corresponding total link flows satisfy
fij < Cij for all
.gif){kind=small}
.
Theorem 1
If a routing matrix .gif){kind=small}
is a fixed point of the analytic model
for the off-policy algorithm, then .gif){kind=small}
yields network flows which correspond
to a Wardrop equilibrium.
Proof
From Figs. (29),
(30)
and (31),
it is straightforward to show that if a routing matrix Ψ is a fixed point
of the off-policy analytic model, then for any link (i, j)
with ψij > 0 (corresponding to a link on a
used path), we have .gif){kind=small}
, and for any link with
ψij = 0 (an unused link), we have .gif){kind=small}
. This condition corresponds to the
qualitative definition of the Wardrop equilibrium given in Section 7.1.
A formal proof from first principles, using standard theory of nonlinear
optimisation, is given in [22]. 
We note that for any given problem instance, membership of the set .gif){kind=small}
is determined by the interaction of the
traffic demands, network topology and link capacities. In particular, if .gif){kind=small}
is empty, then it is impossible to
carry the given traffic demands without violating at least one capacity
constraint. Thus, .gif){kind=small}
essentially contains all “reasonable”
routing matrices, and its hypothesis in Theorem
1 is not restrictive, except in the case of a very poorly-dimensioned
network.
Finally, we note that Wardrop equilibrium routing policies are, by definition, loop-free. Therefore, the off-policy version of the ant-based routing algorithm produces equilibrium routing matrices Ψ which are loop-free for both ants and data packets, without the need for a separate looping-prevention mechanism.
The research presented in this paper raises a number of important issues that need to be addressed in the future development of ant-based and related routing algorithms. In particular, we have identified the on-policy property that is inherent in the current design of ant-based routing algorithms. This property is a result of the fact that the ant and data routing policies are inherently coupled to the ant exploration mechanism, and results in a number of problems and inefficiencies described in Sections Sections 6 and 7.
As a first step towards addressing these issues, we have developed an off-policy version of the ant-based routing algorithm, and we have demonstrated that it is able to achieve routing policies which correspond to a form of user-based optimisation known as Wardrop equilibria. The modifications that we propose result in the de-coupling of the tasks of network exploration, delay estimation and load balancing.
Although simulation models constitute a very valuable research tool in the area of ant-based routing, we have demonstrated that useful insights can be gained through the development and study of an analytical model and its theoretical properties. The work presented in this paper establishes an analytical framework within which ant-based routing algorithms can be modelled, and the authors hope that this will stimulate further theoretical developments.
A useful direction in which to extend our model would be to consider more
complex traffic models. Also, there is a need to establish convergence results
for ant-based routing algorithms. Regarding the latter, the authors expect that
weak convergence to a Wardrop equilibrium (in the case of the off-policy
algorithm) can be shown using the theory of stochastic approximation algorithms
[38].
However, such a convergence result would rely on a separation of time-scales
between the delay estimation and routing update components of the algorithm
(see, for example, [5],
[39]
and [40]),
which in turn would dramatically reduce the rate at which the algorithm is able
to react to sudden network changes. Thus, the tension between conditions which
guarantee convergence, and those which enable a rapid response, is a matter
which deserves further attention.
The authors would like to thank the anonymous referees for their helpful
suggestions in improving the paper. We also thank Peter Taylor for engaging with
us in many helpful discussions, and for his valuable input to the research
presented in this paper. Andre Costa would like to acknowledge the support of
the Australian Research Council Centre of Excellence for Mathematics and
Statistics of Complex Systems. He also acknowledges the receipt of the South
Australian Premier’s Scholarship for Information Technology, and an Australian
Postgraduate Award.
[1] D. Bertsekas and J. Gallager, Data Networks, Prentice Hall, Englewood Cliffs, NJ (1992).
[2] R.S. Sutton and A.G. Barto, Reinforcement Learning: An Introduction, MIT Press, Cambridge, MA (1998).
[3] J. Boyan and M. Littman, Packet routing in dynamically changing networks: a reinforcement learning approach, Advances in Neural Information Processing Systems Vol. 6, Morgan Kaufmann, San Francisco, CA (1993) pp. 671–678.
[4] P. Choi and D. Yeung, Predictive Q-routing: a memory-based reinforcement learning approach to adaptive traffic control. In: S. Touretzky, M. Mozer and E. Hasselmo, Editors, Advances in Neural Information Processing Systems Vol. 8, MIT Press, Cambridge, MA (1996), pp. 945–951.
[5] V.S. Borkar and P. Kumar, Dynamic cesaro-wardrop equilibration in networks, IEEE Transactions on Automatic Control 48 (2003) (3), pp. 382–396. Abstract-INSPEC | Abstract-Compendex | $Order Document | Full Text via CrossRef
[6] E. Bonebeau, M. Dorigo and T. Theraulaz, From Natural to Artificial Swarm Intelligence, Oxford University Press, New York (1999).
[7] M. Dorigo and T. Stutzle, Ant Colony Optimization, MIT Press, Cambridge (2004).
[8] E. Bonebeau, F. Henaux, S. Guerin, D. Snyers, P. Kuntz and G. Theraulaz, Routing in telecommunications networks with “smart ant-like agents, Proceedings of IATA ’98, Second Int. Workshop on Intelligent Agents for Telecommunication Applications, Lecture Notes in AI Vol. 1437, Springer, Berlin (1998).
[9] G. Di Caro and M. Dorigo, AntNet: Distributed stigmergetic control for communications networks, Journal of Artificial Intelligence Research 9 (1998), pp. 317–365.
[10] M. Huesse, D. Snyers, S. Guerin and P. Kuntz, Adaptive agent-driven load balancing in communication networks, Advances in Complex Systems 1 (1998), pp. 237–254.
[11] R. Schoonderwoerd, O. Holland, J. Bruten and L. Rothkrantz, Ant-based load balancing in telecommunications networks, Adaptive Behaviour 5 (1996), pp. 169–207. Abstract-INSPEC | $Order Document
[12] T. White, B. Pagurek and F. Oppacher, Connection management using adaptive mobile agents, Proceedings of the International Conference on Parallel and Distributed Processing Techniques and Applications, CSREA Press (1998).
[13] K. Sim and W. Sun, Ant colony optimisation for routing and load-balancing: survey and new directions, IEEE Transactions on Systems, Man and Cybernetics - Part A: Systems and Humans 33 (2003), pp. 560–573.
[14] S. Thomas, IP Switching and Routing Essentials, Wiley, New York (2002).
[15] M. Osborne and A. Rubenstein, A Course in Game Theory, MIT Press, Cambridge, MA (1994).
[16] D. Bertsekas, Nonlinear Programming, Athena Scientific, Belmont, MA (1999).
[17] J.G. Wardrop, Some theoretical aspects of road traffic research, Proc. Institution of Civil Engineers, Part II 1 (1952), pp. 325–362.
[18] E. Bonebeau, M. Dorigo and T. Theraulaz, Inspiration for optimisation from social insect behaviour, Nature 406 (2000), pp. 39–42.
[19] J. Deneubourg, S. Aron, S. Goss and J. Pasteels, The self-organizing exploratory behaviour of the argentine ant, Journal of Insect Behaviour 3 (1990), pp. 159–168. Full Text via CrossRef
[20] M. Millonas, Swarms, phase, transitions and collective intelligence, Artificial Life III, SFI Studies in the Science of Complexity, Addison-Wesley, Reading, MA (1994).
[21] G. Di Caro, M. Dorigo and L. Gambardella, Ant algorithms for discrete optimization, Artificial Life 5 (1999), pp. 137–172.
[22] A. Costa, Analytic Modelling of Agent-based Network Routing Algorithms, PhD Thesis, School of Applied Mathematics, University of Adelaide, 2003.
[23] L. Kleinrock, Queueing Systems Vol. 1, Wiley, New York (1975).
[24] D. Bertsekas and J. Tsitsiklis, Neuro-Dynamic Programming, Athena Scientific, Belmont, MA (1996).
[25] M. Puterman, Markovian Decision Problems, Wiley, New York (1994).
[26] N. Dunford and J. Schwartz, Linear Operators, Interscience Publishers, New York (1958).
[27] D. Bertsekas, Dynamic Programming and Optimal Control, Vol. II, Athena Scientific, Belmont, MA (1995).
[28] S. Dafermos and F. Sparrow, The traffic assignment problem for a general network, Journal of Research of the National Bureau of Standards 73 (1969), pp. 91–118. Abstract-INSPEC | $Order Document | MathSciNet
[29] T. Boulogne, E. Altman, H. Kameda and O. Pourtallier, Mixed equilibria for multiclass routing games, IEEE Transactions on Automatic Control 47 (2002), pp. 913–916.
[30] Y. Korilis and A. Lazar, On the existence of equilibria in noncooperative optimal flow control, Journal of the ACM 42 (1995) (3), pp. 584–613. Abstract-INSPEC | $Order Document | MathSciNet | Full Text via CrossRef
[31] A. Orda, R. Rom and N. Shimkin, Competitive routing in multi-user communications networks, IEEE/ACM Transactions on Networking 1 (1993), pp. 510–521. Abstract-Compendex | Abstract-INSPEC | $Order Document | Full Text via CrossRef
[32] A. Haurie and P. Marcotte, On the relationship between nash-cournot and wardrop equilibria, Networks 15 (1985), pp. 295–308. Abstract-INSPEC | Abstract-Compendex | $Order Document | MathSciNet
[33] D. Bertsekas, E. Gafni and R. Gallagher, Second derivative algorithms for minimum delay distributed routing in networks, IEEE Transactions on Communications 32 (1984), pp. 911–919. Abstract-INSPEC | $Order Document | MathSciNet | Full Text via CrossRef
[34] D. Cantor and M. Gerla, Optimal routing in a packet-switched network, IEEE Transactions on Computers 23 (1974), pp. 1062–1068.
[35] C. Cassandras, V. Abidi and D. Towsley, Distributed routing with on-line marginal delay estimation, IEEE Transactions on Communications 38 (1990), pp. 348–359. Abstract-INSPEC | Abstract-Compendex | $Order Document | Full Text via CrossRef
[36] R. Gallagher, A minimum delay routing algorithm using distributed computation, IEEE Transactions on Communications 25 (1979), pp. 73–85.
[37] D. Bertsekas, Dynamic behavior of shortest path routing algorithms for communication networks, IEEE Transactions on Automatic Control 27 (1982), pp. 60–74. Abstract-INSPEC | $Order Document | MathSciNet | Full Text via CrossRef
[38] H. Kushner, Stochastic Approximation Algorithms and Applications, Springer, New York (1997).
[39] V.S. Borkar, Asynchronous stochastic approximations, SIAM Journal on Control and Optimization 36 (1998) (3), pp. 840–851. Abstract-Compendex | Abstract-INSPEC | $Order Document | MathSciNet | Full Text via CrossRef
[40]
V. Konda and J. Tsitsiklis, Actor-critic algorithms, SIAM Journal on Control
and Optimisation 42 (2003) (4), pp. 1143–1166. Abstract-INSPEC
| $Order
Document | Full Text via CrossRef
The analytic model presented in Section 5 can be adapted to represent the off-policy version of the ant-based routing algorithm, which is described in Section 8, as follows.
We replace the data routing matrix Ψ(σ, n), with a non-parameterized matrix Ψ(n), which is updated according to the procedure specified in Section 8. The routing matrix Ψ(n) uniquely determines the way in which the data traffic demands si, are routed through the network, thus yielding the data node flows and link flows.
In modelling the ant traffic flows, we must take into consideration the fact
that in the off-policy version of the algorithm, ants perform first hop
exploration, and follow the data routing policy Ψ(n), for all
subsequent link selections. Assume once again that the ant traffic demand
entering the network at node i is given by .gif){kind=small}
. In addition, assume that ants select
their first hop link uniformly at random. It follows that the ant traffic
created at node i, will create a mean traffic flow of k on each
outgoing link .gif){kind=small}
, and so an ant traffic demand of k
at each node .gif){kind=small}
, which is subsequently routed to the
destination according to the data routing policy. The details are presented in
[22].
Taking into account the modified ant traffic flows, as described above, we combine the ant and data traffic flows to obtain the total link flows, fij(n), which in turn give rise to expected link delays, Rij(n). The Q-values are then given by
.gif){kind=small}
is weighted by the data routing
probabilities, reflecting the fact that ants utilize the data routing
probabilities for all link selections subsequent to the first hop. The solution
to the system of equations (33)
can be written in vector form asThe mapping governing the updates of the data routing matrix is obtained in a straightforward manner by indexing the variable quantities in the update rules Figs. (28), (29) and (31) using n = 1, 2, … .
Following the same approach as in Section 5,
we can express the analytic model for the off-policy algorithm using a more
compact notation. We omit the details, which are straightforward, and are given
in [22].
Briefly, we can construct the composite mapping F
, which maps data routing probabilities to Q-values, and
the composite mapping Ω, which maps data routing probabilities and Q-values to
data routing probabilities. The analytic model for the off-policy algorithm can
then be expressed as an iteration of data routing probabilities
Unlike in Section 5,
here it is not possible to express the analytic model as an iteration of
Q-values alone. This is because in the off-policy version, the data
routing probabilities are not directly defined by the Q-values.
Specifically, the mapping Ω* defines an incremental update to the
existing data routing probabilities based on the Q-values, but does not
define the routing probabilities directly from the Q-values, as did the
mapping Ω in Section 5.
Corresponding author. Address: Centre of Excellence for
Mathematics and Statistics of Complex Systems, University of Melbourne,
Melbourne 3010, Australia. Tel.: +61 3 8344 1619; fax: +61 3 8344 4599.  |
Nigel Bean is currently Chair of Applied Mathematics at the University of Adelaide. His previous position was as Director of TRC Mathematical Modelling, a commercially funded research and consulting group that is part of Applied Mathematics at the University of Adelaide. Nigel is the recipient of the 2001 J.H. Mitchell Medal awarded by the Australian and New Zealand Industrial and Applied Mathematics (ANZIAM) division of the Australian Mathematical Society, and the 2003 P.A.P. Moran Medal awarded by the Australian Academy of Science. Nigel was awarded his Ph.D. by the University of Cambridge in 1993 and was supervised by Frank Kelly, FRS. |
.jpg) |
Andre Costa is currently a Research Fellow at the Centre of Excellence for Mathematics and Statistics of Complex Systems at the University of Melbourne. His previous position was Assistant Lecturer in Applied Mathematics at the University of Adelaide. Andre Costa was awarded his PhD in Applied Mathematics by the University of Adelaide in 2003, and was supervised by Nigel Bean and Peter Taylor. |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Volume 49, Issue 2 , 5 October 2005, Pages 243-268 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| Copyright © 2005 Elsevier B.V. All rights reserved. ScienceDirect® is a registered trademark of Elsevier B.V. |
(1-γ)Qik,ik+1,d+γqik,ik+1,d,.gif)
.gif)
.gif){kind=small}
.gif)
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif)
.gif)
.gif){kind=small}
.gif){kind=small}
.gif)
.gif)
.gif)
.gif){kind=small}
.gif)
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif)
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif)
.gif){kind=small}
.gif)
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif)
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif)
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif)
.gif){kind=small}